CBSE 12th Maths 2 Marks Questions: The 2024 board exams are on the horizon, and the mathematics paper will be held on March 9, 2024. Maths is a major subject in class 12 and is opted for by most students in the commerce and science streams. Mathematics is no piece of cake and often ends up troubling the students in the board exams.
Maths requires substantial practice and a clear understanding of the fundamental concepts. You also need good calculation speed and shortcuts for solving questions. This makes a difference in the final exams where some students crumble under the stress and take 5 minutes to solve a question that they would have otherwise cracked in 2 minutes.
Time management, good presentation and correct answers all require practice the CBSE has published multiple resources like sample papers, mock tests and previous years questions to facilitate students. Today, we bring you the most important 2-mark questions of Class 12 mathematics with solutions.
List of 10 Important Questions of 2 Marks for Class 12th Maths with Solutions
Question 1: Find the domain of the function y = cos-1 (|x - 1|). Show your steps.
Answer: Since the domain of inverse of cosine function is [-1, 1], finds the domain of the given function as follows:
-1 ≤ x - 1 ≤ 1
So, 0 ≤ x ≤ 2
And,
-1 ≤ 1 - x ≤ 1
=> 1 ≥ x - 1 ≥ -1
So, 2 ≥ x ≥ 0
Concludes the domain of cos-1 (|x - 1|) as [0, 2].
Question 2: Iqbal, a data analyst in a social media platform is tracking the number of active users on their site between 5 pm and 6 pm on a particular day.
The user growth function is modelled by N(t) = 1000e 0.1t , where N(t) represents the number of active users at time t minutes during that period.
Find how fast the number of active users are increasing or decreasing at 10 minutes past 5 pm. Show your steps.
Answer: Write that the rate at which the number of active users is increasing or decreasing at a given time is given by d/dtN(t).
Finds the derivative of N(t) as: d/dtN(t) = 1000 (0.1) e0.1t Finds the rate of change of active users at 10 minutes past 5 pm as: d/dtN(10) = 1000(0.1)e(0.1)(10) = 100e
Concludes that the number of active users are increasing at a rate of 100e people per minute at 5:10 pm on that day.
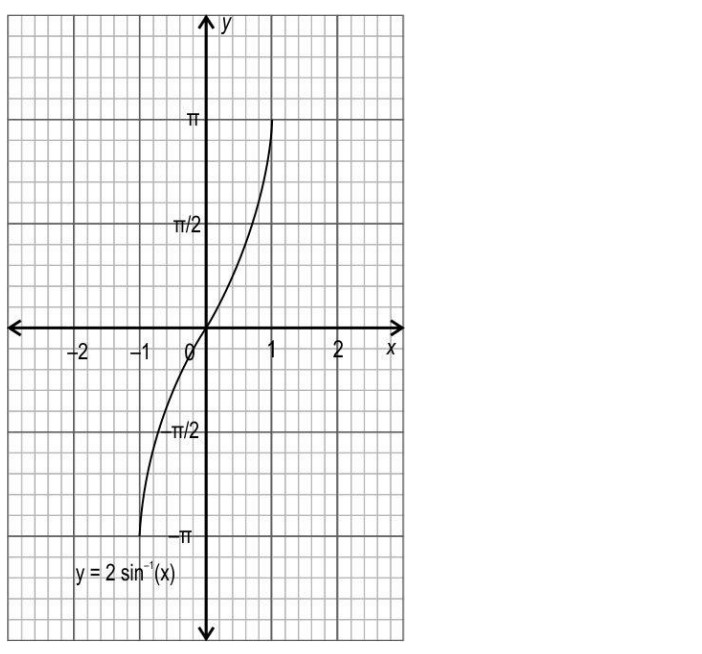
Question 3: Draw the graph of the following function: y = 2sin-1 (x), -π ≤ y ≤ π
Answer: Draws the graphs of y = 2sin-1 (x) as shown below.
Question 4: 
i) What is the equation of this line in cartesian form?
ii) If A’s coordinates are (-2,5,-3), use the cartesian equation of the line to find the coordinates of B.
Answer: 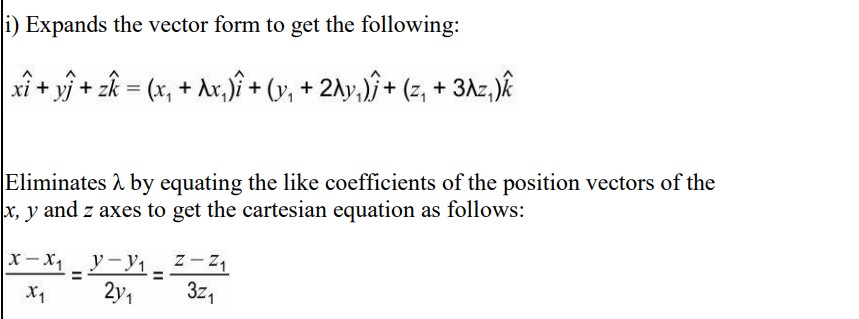
iii) Assumes the coordinates of B as (x2,y2,z2) and compares the cartesian form of the equation from step 2 with the regular form of the cartesian equation to find:
x2=2x1, y2=3y1 and z2=4z1
Substitute values x1 = (-2), y1 = 5 and z1 = (-3) in the equations from step 3 to get coordinates of B as (-4, 15, -12).
Also Read: CBSE Class 12 Maths Board Exam 2024: Check 60 Day Study Plan and Weekly Strategy to Score 95+ Marks
Question 5: Based on the above equation, find tan-1(1/x) using the principal values of the inverse trigonometric functions. Show your work.
Answer: Solves the RHS to obtain 2π/3 as follows:
cos-1(-1)-cosec-1(2/√3)
= π-π/3
= 2π/3
Equates the LHS to obtain x = − 1/√3 as follows:
cot-1(x) = 2π/3
x=cot(2π/3)
x= -(1/√3)
Finds tan−1(1/x) as -π/3 as follows:
tan-1(1/x) = tan-1(-√3)= -π/3
Question 6: 
Answer:
i) Finds the domain as (−∞, 2/5] ∪ [ 4/5,∞)as follows:
5x-3≤-1 or 5x-3≥1
x≤2/5 or x≥4/5
ii) Finds the range as [−2,3π− 2] as follows:
0≤cos-1(1/2x-1)≤π
3(0)-2≤3cos-1(1/2x-1)-2≤3(π) -2
3(0)-2≤y≤3(π)-2
-2≤y≤3π-2
Question 7: If A is a square matrix such that A2 = I, then find the simplified value of (A – I)3 + (A + I)3 – 7A.
Answer:
Given, A2 = 7 ……. (i)
Now, (A – I)3 + (A + I)3 – 7A
= (A3 – 3A2I + 3AI2 – I) + (A3 + 3A2I + 3AI2 + I3) – 7A
= A3 – 3A2 + 3AI – I + A3 + 3A2 + 3AI + I – 7A
[∵ A2I = A2 and I3 = I3 = I]
= 2A3 + 6AI – 7A = 2A2 A + 6A – 7A [∵ AI = A]
= 2IA – A [from Eq. (1)]
= 2A – A = A [∵ IA = A]
Question 8: Find the maximum profit that a company can make, if the profit function is given by P(x)=72+42x-x2, where x is the number of units and P is the profit in rupees.
Answer: For maxima and minima, P’(x)=0 => 42-2x=0
=> x=21 and P’’(x)= -2<0
So, P(x) is maximum at x=21.
The maximum value of P(x)= 72+(42x21)-(21)2 = 513 i.e., the maximum profit is 513.
Question 9: Prove that if E and F are independent events, then the events E and F’ are also independent.
Answer: Given, E and F are independent events, therefore
⇒ PE( ∩ F) = P(E) P(F) …….. (i)
Now, we have,
P(E ∩ F’) + P(E ∩ F) = P(E)
P(E ∩ F’) = P(E) – P(E ∩ F)
P(E ∩ F’) = P(E) – P(E ) P(F) [using Eq. (i))
P(E ∩ F’) = P(E) [1 – P(F)]
P (E ∩ F’) = P(E ) P(F’)
∴ E and F ‘are also independent events.
Hence proved.
Question 10: 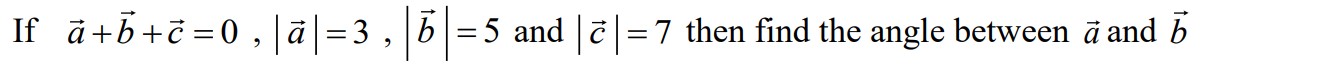
Answer: 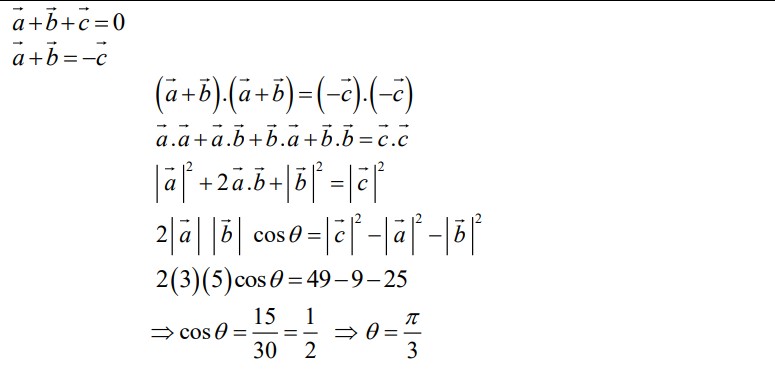
You can download the questions in PDF format below.
CBSE Class 12 Mathematics Important 2 Marks Questions |
CBSE asks 5 very short answer-type questions in the board exam under 2 mark segment, The section has been named as Section B. Under this section, the board will ask short questions to students that can be answered within 10 minutes at maximum.
Recommended:
